Area av en cirkel: formel. Varför är arean av en cirkel beskriven och inskriven i en kvadrat lika med en rätvinklig likbent triangel, en rätvinklig, likbent trapets?

Hur hittar man arean av en cirkel? Hitta först radien. Lär dig lösa enkla och komplexa uppgifter.

En cirkel är en sluten kurva. Varje punkt på cirkellinjen kommer att vara lika långt från mittpunkten. En cirkel är en platt form, så det är enkelt att lösa uppgiften att hitta området. I den här artikeln kommer vi att överväga hur man hittar arean av en cirkel inskriven i en triangel, trapets, kvadrat och beskrivs nära dessa figurer.

Area av en cirkel: formel med radie, diameter, längd på en cirkel, problemlösningsexempel

För att hitta arean av en figur måste du veta att det är radien, diametern och talet π.

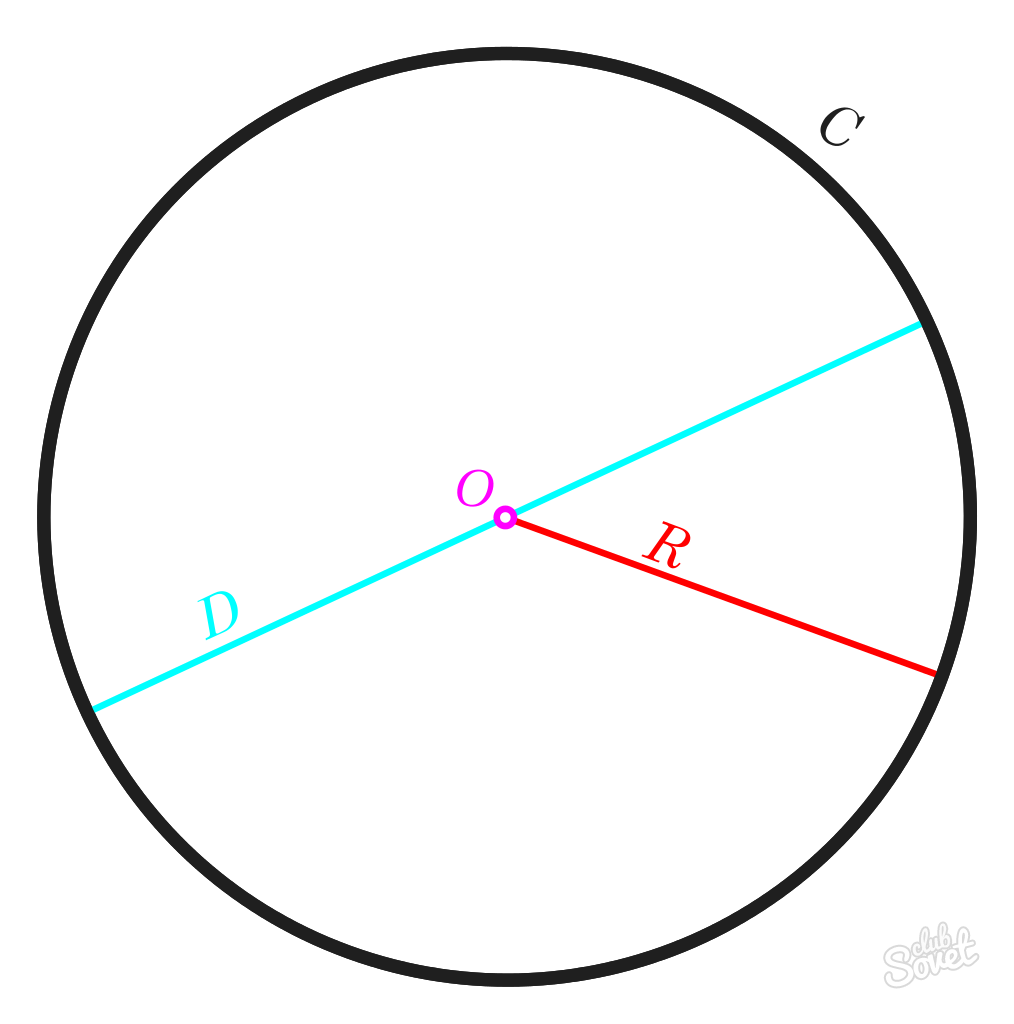
Radie R är avståndet som begränsas av cirkelns mittpunkt. Längden på alla R-radier i en cirkel kommer att vara lika.

Diameter D är en linje mellan två valfria punkter på en cirkel som går genom mittpunkten. Längden på detta segment är lika med längden på R-radien multiplicerat med 2.

Talet π är ett konstant värde lika med 3,1415926. I matematik avrundas detta tal vanligtvis uppåt till 3,14.

Formeln för att hitta arean av en cirkel genom radien:

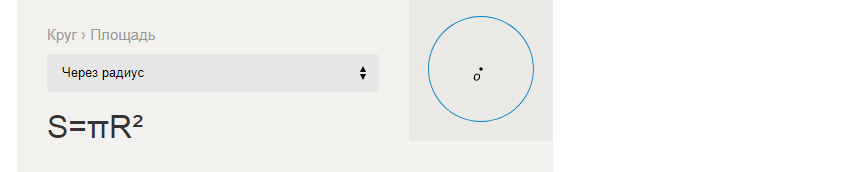
Exempel på att lösa uppgifter för att hitta S-arean av en cirkel genom R-radien:

---------- ---------------------------- --

Uppgift: Hitta arean av en cirkel, om dess radie är 7 cm.

Lösning: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Svar: Arean av en cirkel är 153,86 cm2.

Formeln för att hitta S-arean av en cirkel genom D-diametern:

Exempel på att lösa uppgifter för att hitta S om D är känt:

---------- ----------------------------------

Uppdrag: Hitta S i en cirkel, om dess D är lika med 10 cm.

Lösning: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Svar: Arean av en platt rund figur är 78,5 cm2.

Hitta S för en cirkel, om cirkelns längd är känd:

Först hittar vi vad radien är. Längden på cirkeln beräknas med formeln: L=2πR, följaktligen kommer radien R att vara lika med L/2π. Nu hittar vi cirkelns area med hjälp av formeln genom R.

Låt oss överväga lösningen på exemplet med problemet:

) ------------------ ------------------------------------

Uppgift: Hitta arean av en cirkel, om längden på cirkeln L är känd — 12 cm.

Lösning: Först hittar vi radien: R=L/2π=12/2*3.14=12/6.28=1.91.

Nu hittar vi arean genom radien: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Svar: Arean av en cirkel är 11,46 cm2.

Area av en cirkel inskriven i en kvadrat: formel, exempel på att lösa problem

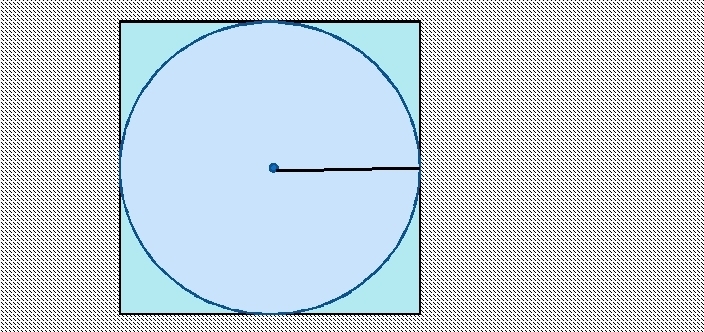
Att hitta arean av en cirkel inskriven i en kvadrat är enkelt. Sidan på kvadraten är cirkelns diameter. För att hitta radien måste du dividera sidan med 2.

Formeln för att hitta arean av en cirkel inskriven i en kvadrat:

Exempel på att lösa problem för att hitta arean av en cirkel inskriven i en kvadrat:

-- ---------------------------------- ----

Uppgift nr 1: Sidan på en kvadratisk figur, som är lika med 6 centimeter, är känd. Hitta S-området för den inskrivna cirkeln.

Lösning: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Svar: Arean av en platt rund figur är 28,26 cm2.

------------------------------------------ -----------

Uppgift #2 :Hitta S för en cirkel inskriven i en kvadratisk figur och dess radie om en sida är lika med a=4 se

Lös enligt följande : Först hittar vi R=a/2=4/2=2 se

Nu kommer vi att hitta arean av cirkeln S=3,14*22=3,14*4=12,56 cm2.

Svar: Arean av en platt rund figur är 12,56 cm2.

Area av en cirkel omskriven om en kvadrat: formel, exempel på problemlösning

Det är lite svårare att hitta arean av en rund figur som beskrivs runt en kvadrat. Men genom att känna till formeln kan du snabbt beräkna detta värde.

Formel för att hitta S i en cirkel omskriven kring en kvadratisk figur:

Exempel på att lösa problem för att hitta arean av en cirkel som beskrivs runt en kvadratisk figur:

) Problem

Area av en cirkel inskriven i en rät och likbent triangel: formel, exempel på att lösa problem

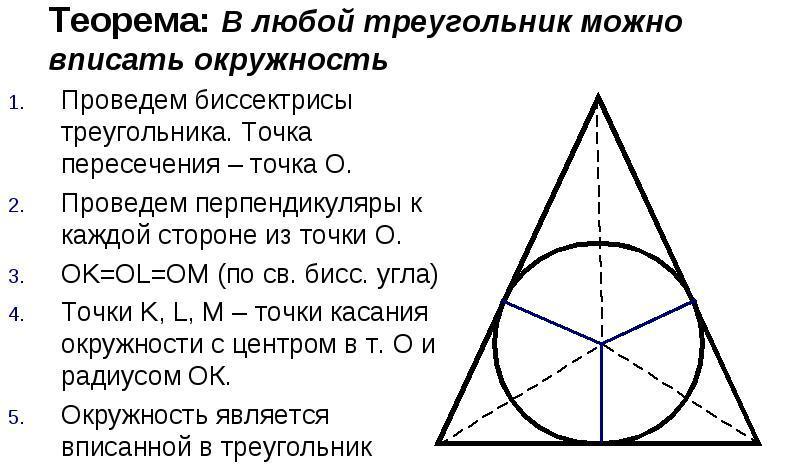
En cirkel inskriven i en triangulär figur är en cirkel som berör alla tre sidorna av triangeln. Vilken triangulär figur som helst kan inskrivas med en cirkel, men bara en. Cirkelns centrum kommer att vara skärningspunkten för triangelns vinkelhalveringslinje.

Formel för att hitta arean av en cirkel inskriven i en likbent triangel:

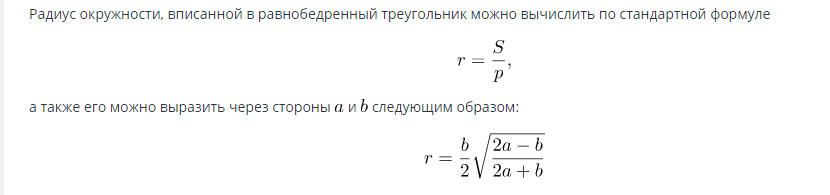
När radien är känd kan arean beräknas med formeln: S=πR2.

Formel för att hitta arean av en cirkel inskriven i en rätvinklig triangel:

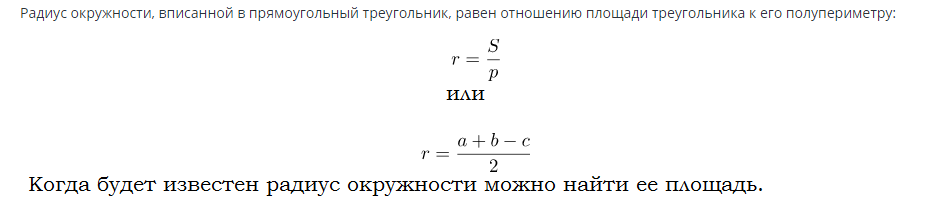
Exempel på problemlösningar:

Problem # 1

)

Om du i det här problemet också behöver hitta arean av en cirkel med en radie på 4 cm, kan du göra det med formeln: S=πR2

Uppgift #2

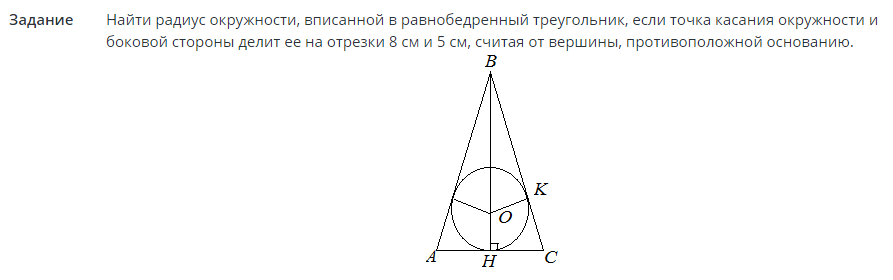
Lösningar:

Nu när radien är känd kan cirkelns area hittas i termer av radien. Se formeln ovan i texten.

Uppgift #3

Arean av en cirkel omskriven om en rätvinklig och likbent triangel: formel, exempel på problemlösning

Alla formler för att hitta arean av en cirkel kokar ner till det faktum att du först måste hitta dess radie. När radien är känd är det enkelt att hitta området, som beskrivits ovan.

​

Arean av en cirkel omskriven kring en rätvinklig och likbent triangel hittas av följande formel:

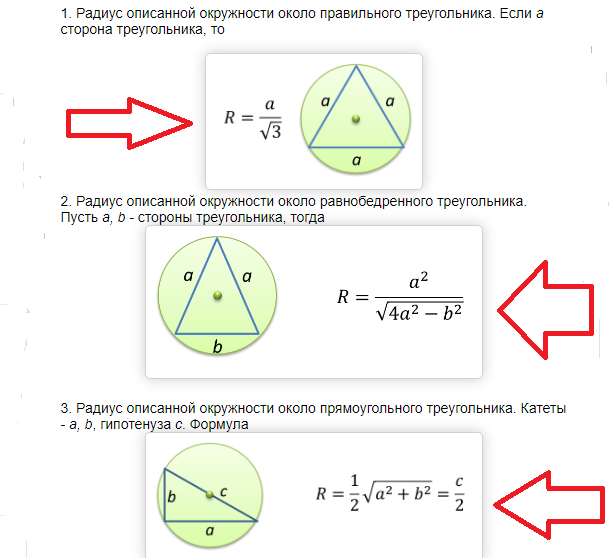
Exempel på problemlösning:

Här är ett annat exempel på att lösa en problem med att använda Herons formel.

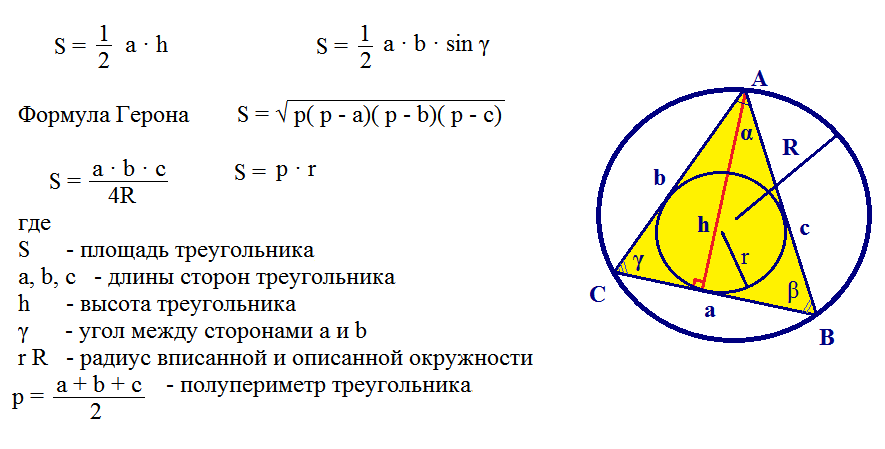
Det är svårt att lösa liknande problem, men de kan övervinnas om du kan alla formler. Elever löser sådana uppgifter i 9:an.

Arean av en cirkel inskriven i en rektangulär och likbent trapets: formel, problemlösningsexempel

Till exempel är en likbent trapets inskriven med en cirkel som är i kontaktpunkten delar en sida i segment m och n.

För att lösa detta problem måste du använda följande formler:

Att hitta arean av en cirkel inskriven i en rektangulär trapets utförs enligt följande formel:

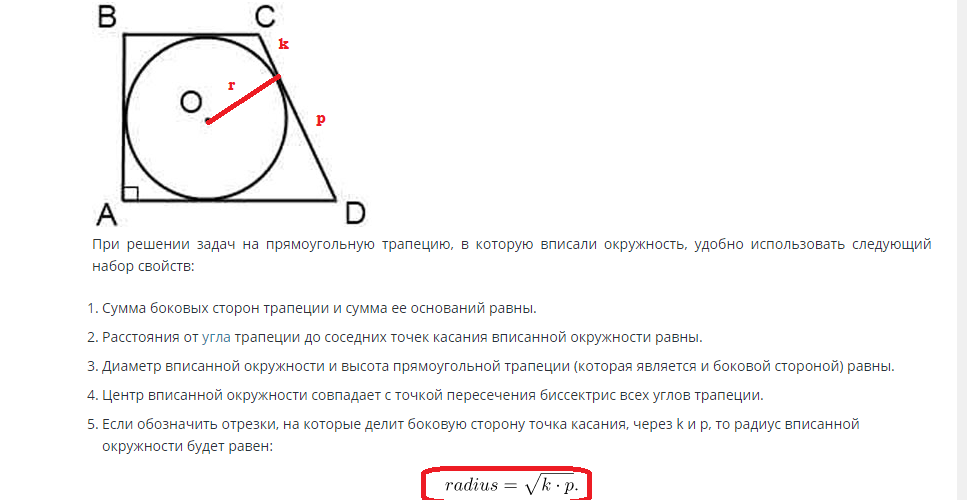
Om sidan är känd, kan radien hittas genom detta värde. Höjden på sidan av trapetsen är lika med diametern på cirkeln, och radien är halva diametern. Följaktligen är radien lika med R=d/2.

Exempel på att lösa problem:

Area av en cirkel omskriven om en rätvinklig och likbent trapets: formel, problemlösningsexempel

En trapets kan inskrivas i en cirkel när summan av de motsatta vinklarna är 180°. Därför kan endast en liksidig trapets vara inskriven. Radien för att beräkna arean av en cirkel som beskrivs nära en rektangulär eller likbent trapetsoid beräknas med hjälp av följande formler:

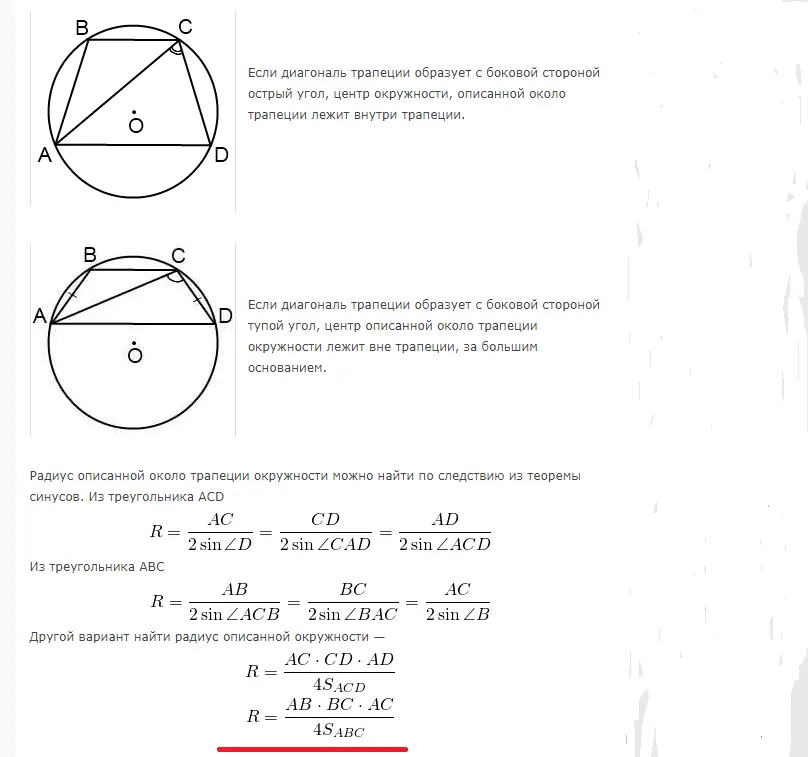
Exempel på problemlösning:

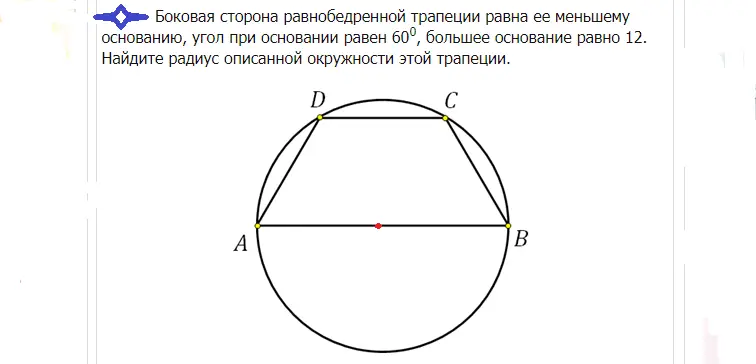
Lösning: Den stora basen går i detta fall genom centrum, eftersom en likbent trapets är inskriven i cirkeln. Mitten delar denna bas exakt på mitten. Om basen AB är lika med 12, så kan radien R hittas enligt följande: R=12/2=6.

Svar: Radien är 6.

Inom geometri är det viktigt att kunna formler. Men det är omöjligt att komma ihåg alla, så även på många tentor är det tillåtet att använda en speciell blankett. Det är dock viktigt att kunna hitta rätt formel för att lösa det eller det problemet. Öva på att lösa olika problem för att hitta radien och arean av en cirkel för att korrekt kunna ersätta formler och få korrekta svar.

Video: Matematik | Beräkning av arean av en cirkel och dess delar